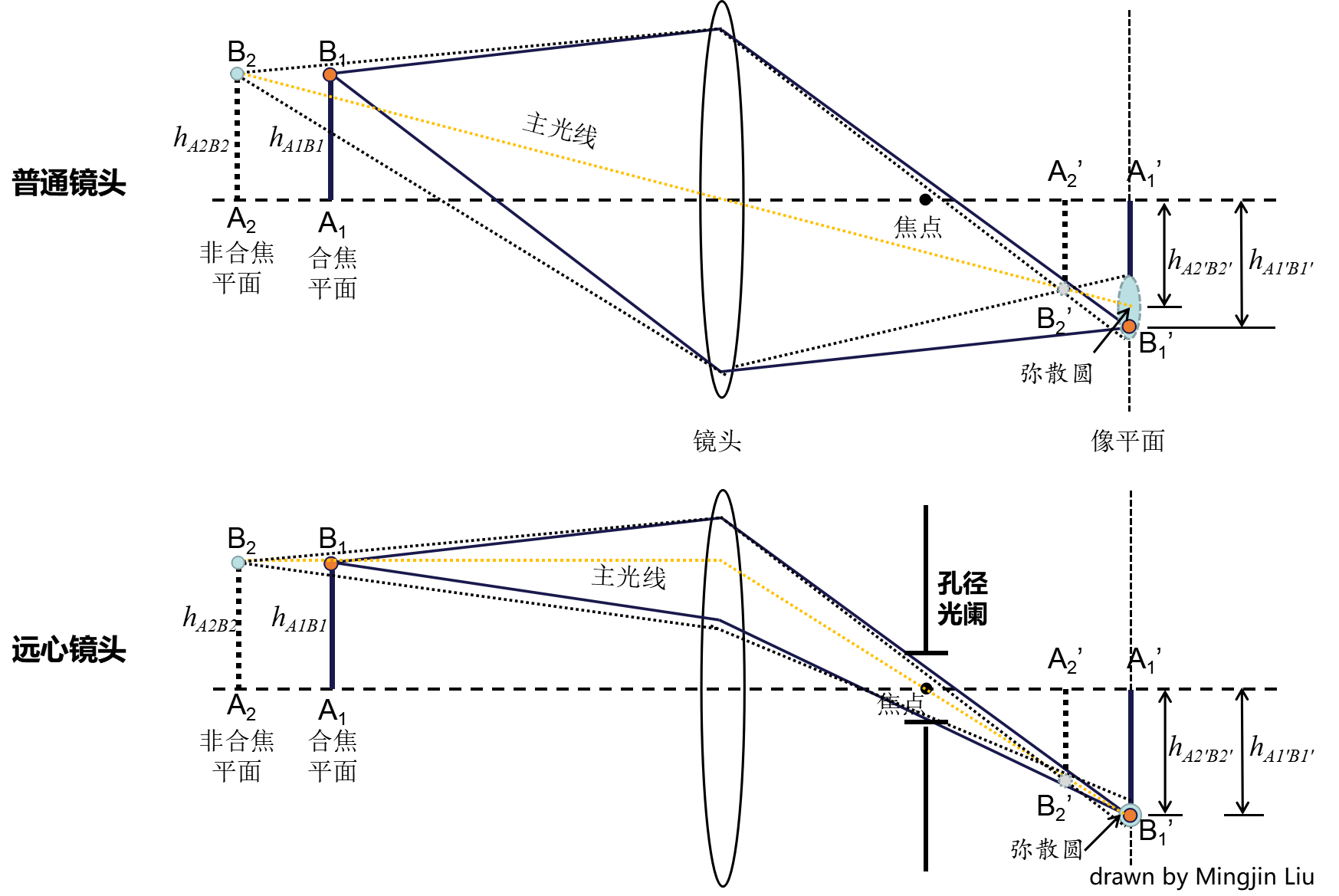
三阶像差理论

什么是三阶像差，为什么是三阶？

像差是实际成像与理想成像之间的差距。三阶像差指的是在求解光学哈密顿正则方程时，保留求解结果的三阶泰勒展开项相对近轴光学结果（仅保留一阶泰勒展开）所产生的额外偏差。

对于旋转对称系统，其光学哈密顿量可以表示为：
\begin{align*}H&=-[n^2(U,z)-V]^2\\ U&=X^2+Y^2\\ V&=P^2+Q^2\end{align*}
其中X和Y是光线在弧矢和子午面上的投影，z是光线的轴向位置，P和Q是光线沿弧矢和子午面上的光学方向余弦。
此时光学哈密顿方程可以写为：
\begin{align*} \frac{dX}{dz}=2P\frac{\partial H}{\partial V},\quad \frac{dP}{dz}=-2X\frac{\partial H}{\partial U} \end{align*}

这里仅写了弧矢面上的，子午面上还有两个方程，将X替换为Y即可。

为了求解方程，需给定边界条件：
\begin{align*} X(z_0)&=x_0,\quad X(\zeta)=\xi\\ Y(z_0)&=y_0,\quad\ Y(\zeta)=\eta \end{align*}
求解方程的结果 $X,Y,P,Q$ ，必定是包含 $x_0,y_0,\xi,\eta$ 的一般式子，并且结果可以按照幂级数展开（泰勒展开）：
\begin{align*} X=X_1+X_2+X_3+\cdot\cdot\cdot,\quad Y=Y_1+Y_2+Y_3+\cdot\cdot\cdot \end{align*}
考虑旋转对称性，结果仅包含奇次幂，因此
\begin{align*} X=X_1+X_3+\cdot\cdot\cdot,\quad Y=Y_1+Y_3+\cdot\cdot\cdot \end{align*}
仅保留一次幂的结果为傍轴近似结果，保留三次幂的结果则考虑了三阶像差。

为了求解光学哈密顿方程，还需要将光学哈密顿量用幂级数展开：
\begin{align*} H=H_0+H_1U+H_2V+\frac{1}{2}(H_{11}U^2+2H_{12}UV+H_{22}V^2)+\cdot\cdot\cdot \end{align*}
将展开后的 $X,Y,H$ 代入光学哈密顿方程
\begin{align*} (\dot{X}_1+\dot{X}_3+\cdot\cdot\cdot)=2(P_1+P_3+\cdot\cdot\cdot)(H_2+H_{12}U+H_{22}V+\cdot\cdot\cdot) \end{align*}

注意到
\begin{align*} U&=X^2+Y^2=(X_1+X_2+X_3+\cdot\cdot\cdot)^2+(Y_1+Y_2+Y_3+\cdot\cdot\cdot)^2\\ &=U_1+2(X_1X_3+Y_1Y_3)+\text{higher-order terms}\\ V&=V_1+2(P_1P_3+Q_1Q_3)+\text{higher-order terms} \end{align*}

光学哈密顿方程又可以进一步写成
\begin{align*} (\dot{X}_1+\dot{X}_3+\cdot\cdot\cdot)=&2(P_1+P_3+\cdot\cdot\cdot)\\ &\times \{ H_2+H_{12}[U_1+2(X_1X_3+Y_1Y_3)+\cdot\cdot\cdot] \\ &+H_{22}[V_1+2(P_1P_3+Q_1Q_3)+\cdot\cdot\cdot]+\cdot\cdot\cdot\} \end{align*}
根据同阶系数相等（类似微扰法），可以得到一阶和三阶的光学哈密顿方程：
\begin{align*} \dot{X}_1&=2H_2P_1\\ \dot{X}_3&=2H_2P_3+2(H_{12}U_1+H_{22}V_1)P_1\\ \dot{P}_1&=-2H_1X_1\\ \dot{P}_3&=-2H_1X_3-2(H_{11}U_1+H_{12}V_1)X_1 \end{align*}

求解上述方程非常复杂，这里只简要提一下思路：

构建一个射线光学传输模型，讨论两种特殊的光线解

两种特殊光线的边界条件分别是：
\begin{align*} X_1(z_0)&=0,\quad Y_1(z_0)=0,\quad X_1(\zeta)=1,\quad Y_1(\zeta)=0,\quad \text{(轴光线)}\\X_1(z_0)&=1,\quad Y_1(z_0)=0,\quad X_1(\zeta)=0,\quad Y_1(\zeta)=0 ,\quad \text{(场光线)}\end{align*}
轴光线的解设为 $X_1(z)\equiv g(z),P_1(z)\equiv \vartheta(z)$ ；场光线的解设为 $X_1(z)\equiv G(z),P_1(z)\equiv \theta(z)$
则对于边界条件为 $X_1(z_0)=x_0,Y_1(z_0)=y_0,X_1(\zeta)=\xi,Y_1(\zeta)=\eta$ 的情况，有一般解（两种特殊光线解的线性叠加）
\begin{align*} X_1(z)=x_0G(z)+\xi g(z),\quad Y_1(z)=y_0G(z)+\eta g(z) \end{align*}
对轴光线和场光线可以列出光学哈密顿方程：
\begin{align*} \dot{g}=2H_2\vartheta,\quad \dot{\vartheta}=-2H_1g\\ \dot{G}=2H_2\theta,\quad \dot{\theta}=-2H_1G \end{align*}
一般光线的动量解
\begin{align*} P_1(z)=x_0\theta(z)+\xi \vartheta(z),\quad Y_1(z)=y_0\theta(z)+\eta \vartheta(z) \end{align*}
上面求解了 $X_1,P_1$ ，现在要求解三阶项 $X_3,P_3$
\begin{align*} \dot{X}_3&=2H_2P_3+2(H_{12}U_1+H_{22}V_1)P_1\\ \dot{P}_3&=-2H_1X_3-2(H_{11}U_1+H_{12}V_1)X_1 \end{align*}
代入轴光线场光线的光学哈密顿方程
\begin{align*}\dot{X}_3\vartheta-\dot{g}P_3=2(H_{12}U_1+H_{22}V_1)P_1\vartheta\\ X_3\dot{\vartheta}-g\dot{P}_3=2(H_{11}U_1+H_{12}V_1)X_1g \end{align*}
相加并积分得到
\begin{align*} \left. (X_3\vartheta-gP_3) \right |_{z_0}^{z_1}=2\int_{z_0}^{z_1}[(H_{11}U_1+H_{12}V_1)X_1g+(H_{12}U_1+H_{22}V_1)P_1\vartheta]dz \end{align*}
因为 $g(z_0)=X_3(z_0)=g(z_1)=0$
\begin{align*} X_3(z_1)=\frac{2}{\vartheta(z_1)}\int_{z_0}^{z_1}[(H_{11}U_1+H_{12}V_1)X_1g+(H_{12}U_1+H_{22}V_1)P_1\vartheta]dz \end{align*}
又因为
\begin{align*} U_1&=X_1^2+Y_1^2=[x_0G(z)+\xi g(z)]^2+[y_0G(z)+\eta g(z)]^2\\ V_1&=P_1^2+Q_1^2=[x_0\theta(z)+\xi \vartheta(z)]^2+[y_0\theta(z)+\eta \vartheta(z)]^2 \end{align*}
令 $r=x_0^2+y_0^2,\quad t=x_0\xi+y_0\eta,\quad s=\xi^2+\eta^2$
\begin{align*} U_1&=rG^2+2tGg+sg^2\\ V_1&=r\theta^2+2t\theta\vartheta+s\vartheta^2 \end{align*}
将 $U_1,V_1$ 代入 $X_3$ 的解，可以得到一个非常复杂的代数关系式
\begin{align*} X_3(z_1)&=[As+2Bt+(C+D)r]\xi+[Bs+2Ct+Er]x_0\\ Y_3(z_1)&=[As+2Bt+(C+D)r]\eta+[Bs+2Ct+Er]y_0 \end{align*}
其中参数 $A,B,C,D,E$ 分别代表了不同的像差系数，它们是关于场光线轴光线位置动量解和光学哈密顿量泰勒系数的代数积分式。对于一个确定了近轴解的光学系统，所谓的像差是泰勒展开的高阶项相对一阶近似解（近轴解）的偏离。场光线轴光线的参数都已确定，光学哈密顿量也确定，因此 $ABCD$ 四个值也是确定的，像差即偏离 $X_3,Y_3$ 仅是关于 $x_0$ 和 $y_0$ 的函数（ $\xi$ 和 $\eta$ 由场光线求解 $G(\zeta)=0$ 可得）。只考虑三阶像差时，偏离为关于 $x_0$ 和 $y_0$ 的三次型多项式。

三阶像差有哪些，具体物理含义是什么？

上一节提到了五个像差系数，每个像差系数代表着一种具体的像差。考虑物面 $x$ 轴（ $y_0=0$ ）上一束任意光线经过面 $z=\zeta$ ，交点距离轴心为 $\rho$ ，则光线与面的交点坐标为（ $\xi=\rho\cos\phi$ ， $\eta=\rho\sin\phi$ ）， $r=x_0^2,\ t=x_0\rho\cos\phi,\ s=\rho^2$ ，则像差为

\begin{align*} X_3&=A\rho^3\cos\phi+Bx_0\rho^2(2+\cos2\phi)+(3C+D)x_0^2\rho\cos\phi+Ex_0^3\\ Y_3&=A\rho^3\sin\phi+Bx_0\rho^2\sin2\phi+(C+D)x_0^2\rho\sin\phi \end{align*}

球差(轴上像差)

$X_3=A\rho^3\cos\phi,\quad Y_3=A\rho^3\sin\phi$
对于轴上物点（ $x_0=y_0=0$ ），三阶像差仅包含球差。由于 $X_3^2+Y_3^2=(A\rho^3)^2$ ，偏离呈现为一个圆形分布，因此该像差导致光线焦点相对近轴焦点发生位移，如图所示：
Spherical Aberration

慧差（轴外像差）

$X_3=Bx_0\rho^2(2+\cos2\phi),\quad Y_3=Bx_0\rho^2\sin2\phi$
消去 $\phi$ ，得到
$(X_3-2Bx_0\rho^2)^2+Y_3^2=(Bx_0\rho^2)^2$
对于轴外物点( $x=x_0$ )，偏离呈现为一个圆形分布，且圆心在轴外，半径与轴外物点位置成正比。该像差导致光线焦点随着轴外点距离增大发生位移，如图所示：
Coma Aberration

像散和场曲（轴外像差）

$X_3=(3C+D)x_0^2\rho\cos\phi,\quad Y_3=(C+D)x_0^2\rho\sin\phi$
消去 $\phi$ ，得到
\begin{align*} \frac{X_3^2}{[(3C+D)x_0^2\rho]^2}+\frac{Y_3^2}{[(C+D)x_0^2\rho]^2}=1 \end{align*}

偏离呈现一个椭圆，该椭圆的长轴短轴与轴外物点位置成正比。该像差导致光线焦点具有方向性，不同方向聚焦面上的光线聚焦位置发生位移，如图所示：
Astigmatism & Curvature
弧矢面上光线的焦点位置与子午面上的不一样，两焦点的间距为 $2Cx_0^2d$ ，其中 $d$ 为出瞳到像面的距离。当 $C=0$ 时，像散为0，因此该两焦点的间距即为像散的度量。当 $C=-D/2$ 时，像点仅在像面上呈现圆形，此时对应场曲为0。对于一个放大倍率为 $M$ 的光学系统，子午方向和弧矢方向的弯曲半径分别为：
\begin{align*} \frac{1}{R_\mathrm{T}}=\frac{2d}{M^2}(3C+D),\quad \frac{1}{R_\mathrm{S}}=\frac{2d}{M^2}(C+D) \end{align*}
该两半径的调和平均值（倒数平均值）即为场曲的度量：
\begin{align*} \frac{1}{R}=\frac{1}{2}\left( \frac{1}{R_\mathrm{T}}+\frac{1}{R_\mathrm{S}} \right)=\frac{2d}{M^2}(2C+D) \end{align*}

畸变（轴外像差）

$X_3=E(x_0^2+y_0^2)x_0,\quad Y_3=E(x_0^2+y_0^2)y_0$
实际像点 $(x_1=Mx_0+E(x_0^2+y_0^2)x_0,\ y_1=My_0+E(x_0^2+y_0^2)y_0)$ ， $M$ 是系统放大倍率。
该像差导致不同位置的物点在像面上放大倍率不一样，如图所示:
Distortion
当考虑像差时，需要同时考虑所有三阶像差，得到的结果是所有三阶像差的组合。
将三阶像差完整公式中的 $2\phi$ 消去，写成平方和的形式：
\begin{align*} \{X_3-2Bx_0\rho^2-Ex_0^3-&[A\rho^3+(3C+D)x_0^2\rho]\cos\phi\}^2\\ &+\{ Y_3-[A\rho^3+(C+D)x_0^2\rho]\sin\phi \}^2=(Bx_0\rho^2)^2 \end{align*}
该公式可以看成一个圆，半径为 $Bx_0\rho^2$ 。圆心在一个椭圆之上，椭圆长短轴为 $A\rho^3+(3C+D)x_0^2\rho,\ A\rho^3+(C+D)x_0^2\rho$ 。椭圆中心在 $(2Bx_0\rho^2+Ex_0^3,\ 0)$ 处，轨迹类似摆线，以圆上一点，绕运动的圆心旋转的轨迹，如图所示：
Combination of Aberration