MZI实现波分和解波分复用

利用MZI实现波分和解波分复用依据的理论是干涉理论，根据上下臂的相位分配可以控制输出光相干相长或相消。

对于一个X_Coupler，其传输矩阵可以写为如下形式：

T(f)=(1−αjαjα1−α)(1)T(f)= \left( \begin{matrix} \sqrt{1-\alpha} & j\sqrt{\alpha}\\ j\sqrt{\alpha} & \sqrt{1-\alpha} \end{matrix} \right)\tag{1}

其中α\alpha为上臂功率占总功率的比值。

一个完整的二端口MZI复用器由两个X_Coupler组成，中间经由两路臂长不等的光路实现相位调控，总体传输矩阵可以写为如下形式：

T(f)=(1−α2jα2jα21−α2)(e−j2π(f−fc)τ001)(ejϕupper00ejϕlower)(1−α1jα1jα11−α1)(2)T(f)= \left( \begin{matrix} \sqrt{1-\alpha_2} & j\sqrt{\alpha_2}\\ j\sqrt{\alpha_2} & \sqrt{1-\alpha_2} \end{matrix} \right) \left( \begin{matrix} e^{-j2\pi(f-f_c)\tau} & 0\\ 0 & 1 \end{matrix} \right) \left( \begin{matrix} e^{j\phi_\mathrm{upper}} & 0\\ 0 & e^{j\phi_\mathrm{lower}} \end{matrix} \right) \left( \begin{matrix} \sqrt{1-\alpha_1} & j\sqrt{\alpha_1}\\ j\sqrt{\alpha_1} & \sqrt{1-\alpha_1} \end{matrix} \right)\tag{2}

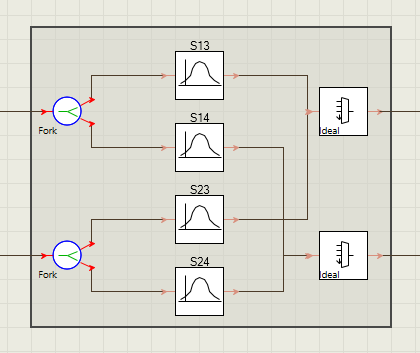
其vtmg结构图

MZI由两个X_Coupler和两个延迟臂构成
  1. PhaseShift_Upper与PhaseShift_Lower为上下两臂的本征相移，由臂长所控制。对于输入单一波长，DelayTime为0，这是因为单一通道内仅存在一个波长，同一波长内无相对时延。
  2. 如果上下输入波长不同，此时ChannelFrequency为上路波长，输入经过第一个X_Coupler后，会按照α\alpha比例分别送入上下两臂，这意味着单一通道内同时存在两个波长，不同波长之间会存在相对时延DelayTime。
  3. 对于上路波长，由于其值等于ChannelFrequency，因此式（2）中第二个矩阵退化为单位矩阵，上路波长仅考虑两臂的PhaseShift。对于下路波长，由于其值与ChannelFrequency存在偏差，因此根据相对时延可以获得下路波长的相移，最后在输出的上下端口获得不同波长的功率分布。
  4. 如果想让左上的光汇聚于右下，则PhaseShift_Lower-PhaseShift_Upper等于π\pi的偶数倍，若汇聚于右上，则为π\pi的奇数倍。在这个基础上想让左下的光汇聚于右下，则设置DelayTime使得e−j2π(f−fc)τ=−1e^{-j2\pi(f-f_c)\tau}=-1，2π(f−fc)τ=(2k+1)π2\pi(f-f_c)\tau=(2k+1)\pi，τ=2k+12(f−fc)\tau=\frac{2k+1}{2(f-f_c)}。

四合一一分四的基于MZI的完整波分\解波分复用vtmu结构图如下

WDM 完整结构图

四合一波分复用结果（上）与解复用结果（下）如下

复用与解复用结果

同一颜色代表同一通道，四路波长分别为1271 nm，1291 nm，1311 nm和1331 nm。