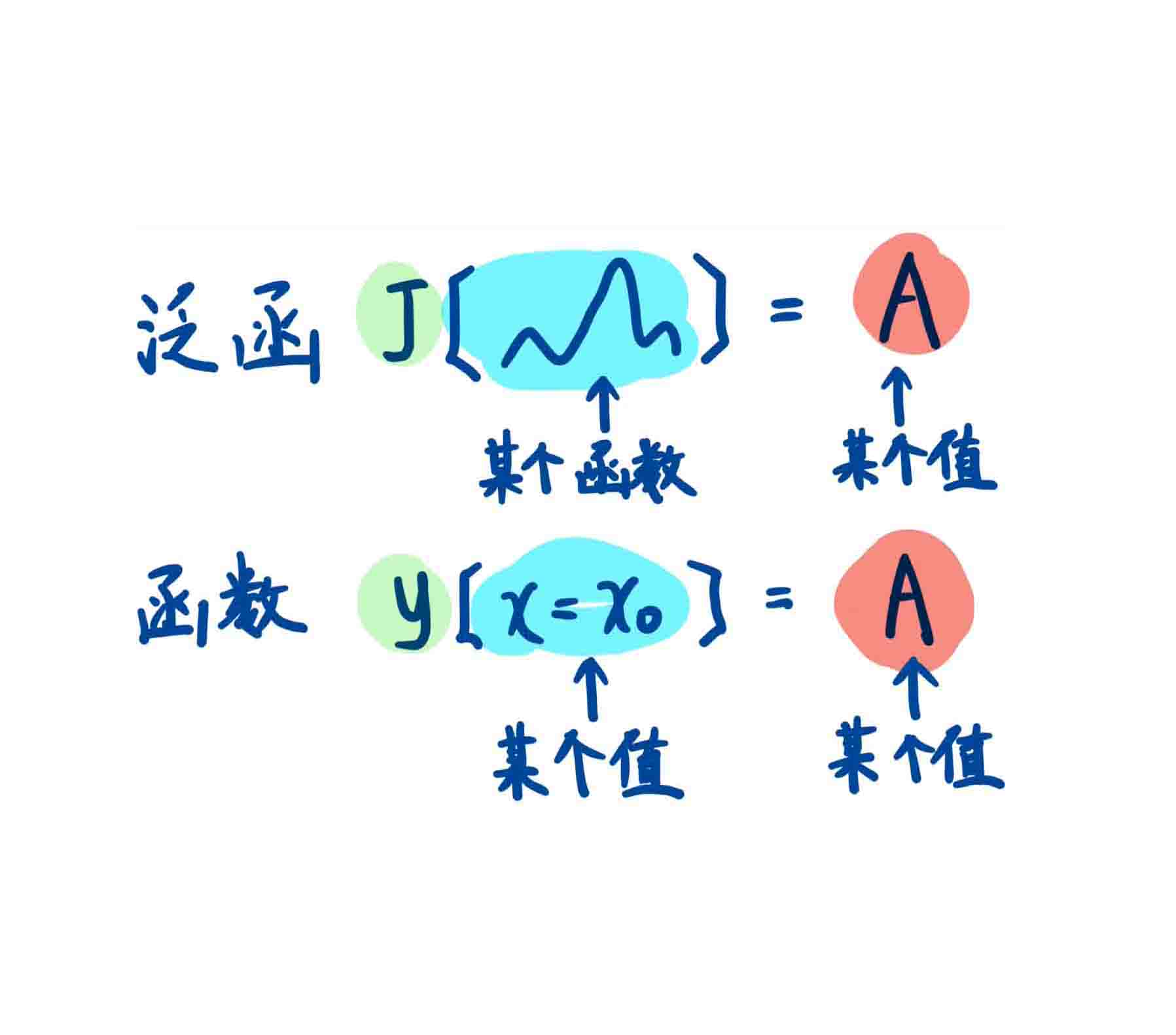
光学哈密顿量

光学哈密顿量

根据光学拉格朗日方程组$\frac{d}{dz}(\frac{\partial L}{\partial\dot{x}})=\frac{\partial L}{\partial x},\quad \frac{d}{dz}(\frac{\partial L}{\partial\dot{y}})=\frac{\partial L}{\partial y}$和哈密顿力学中广义动量的定义$p_j=\frac{\partial L}{\partial \dot{q}_j}$，我们可以在子午方向（y方向）和弧矢方向（x方向）上定义光学广义动量：
\begin{align*} p=\frac{\partial L}{\partial \dot{x}},\quad q=\frac{\partial L}{\partial \dot{y}} \end{align*}

将拉格朗日量带入光学广义动量中
\begin{align*} p=\frac{n\dot{x}}{(1+\dot{x}^2+\dot{y}^2)^{1/2}}=n\frac{dx}{ds},\quad q=\frac{n\dot{y}}{(1+\dot{x}^2+\dot{y}^2)^{1/2}}=n\frac{dy}{ds} \end{align*}

这里我们定义$p$和$q$为光学方向余弦，它们也是光学广义动量。

结合哈密顿量的表象，可以列出光学哈密顿量的公式为

\begin{align*} H=p\dot{x}+q\dot{y}-L(x,y,\dot{x},\dot{y},z) \end{align*}

对光学哈密顿量进行全微分

\begin{align*} dH&=\left( p-\frac{\partial L}{\partial\dot{x}} \right)d\dot{x}+\left( q-\frac{\partial L}{\partial\dot{y}} \right)d\dot{y}+\dot{x}dp+\dot{y}dq-\frac{\partial L}{\partial x}dx-\frac{\partial L}{\partial y}dy-\frac{\partial L}{\partial z}dz \\ &=\dot{x}dp+\dot{y}dq-\dot{p}dx-\dot{q}dy-\frac{\partial L}{\partial z}dz \end{align*}

由此得到光学哈密顿方程组：

\begin{align*} \dot{x}=&\partial H/\partial p,\qquad \ \dot{y}=\partial H/\partial q \\ \dot{p}=&-\partial H/\partial x,\quad \dot{q}=-\partial H/\partial y \\ \partial H/\partial z=&-\partial L/\partial z \end{align*}

将光学广义动量$p$和$q$，以及光学拉格朗日量$L$的表达式代入光学哈密顿量$H$的公式中
\begin{align*} H=&\frac{n\dot{x}}{(1+\dot{x}^2+\dot{y}^2)^{1/2}}\dot{x}+\frac{n\dot{y}}{(1+\dot{x}^2+\dot{y}^2)^{1/2}}\dot{y}-n(1+\dot{x}^2+\dot{y}^2)^{1/2}\\ =&-\frac{n}{(1+\dot{x}^2+\dot{y}^2)^{1/2}}\\ =&-[n^2(x,y,z)-p^2-q^2]^{1/2} \end{align*}

对于一个旋转对称系统（圆柱形透镜），令$u=x^2+y^2,v=p^2+q^2$，对应光学哈密顿量$H=-[n^2(u,z)-v]^{1/2}$

对上述光学哈密顿量在$u,v$上进行泰勒展开：
\begin{align*} H(u,v,z)=H_0(z)+[H_1(z)u+H_2(z)v]+\cdot\cdot\cdot \end{align*}
其中
\begin{align*} H_1(z)=\left.\frac{\partial H}{\partial u}\right |_{u=0,v=0},\quad H_2(z)=\left.\frac{\partial H}{\partial v}\right |_{u=0,v=0} \end{align*}

傍轴近似就是光学哈密顿量在广义坐标维度和广义动量维度进行泰勒展开后仅保留一阶项的操作，需要计算像差时就要保留高阶项进行分析。

根据光学哈密顿方程组，$u$与$x$，$v$与$p$的关系式
\begin{align*} \dot{x}=\partial H/\partial p=2p\frac{\partial H}{\partial v}=2pH_2,\quad \dot{p}=-\partial H/\partial x=-2x\frac{\partial H}{\partial u}=-2xH_1 \end{align*}
求解上述方程组即可得到傍轴近似下的光线路径。