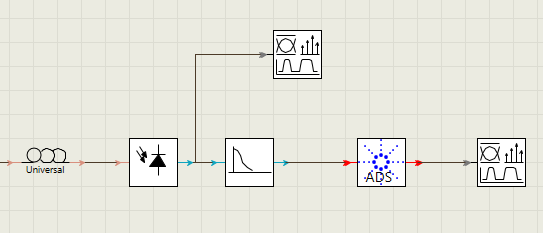
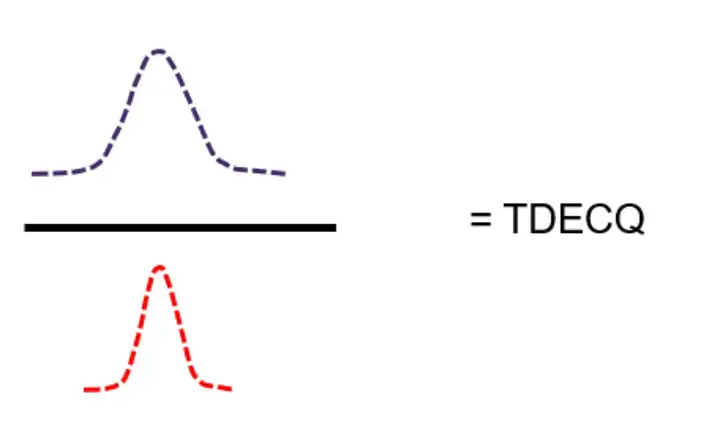
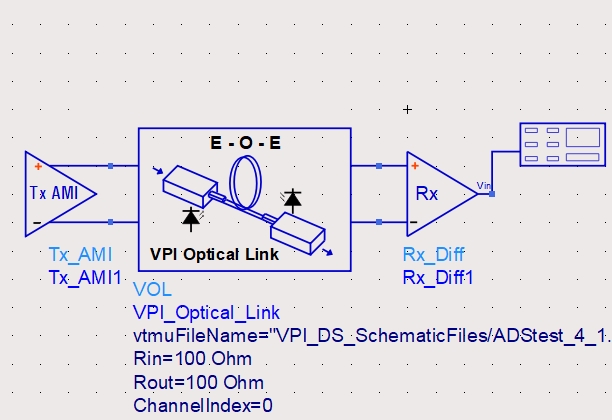
S参数与阻抗匹配

S参数

S参数又称散射参数，描述了电气系统中端口之间的输入输出关系。在高频输入输出中，用波而不是电压或电流来描述给定的网络。因此，在S参数中使用功率波。

在RF设计中，无法使用其他参数进行分析，例如Z，Y，H参数，因为我们无法进行短路和开路分析，所以使用S参数描述待测系统（DUT，Device Under Test）至关重要。对于双端口网络，S参数可以定义为：

$\begin{aligned} \left.S_{11}=\frac{\text{out}_1}{\text{in}_1}\right|_{\text{in}_2=0}\qquad\left.S_{12}=\frac{\text{out}_1}{\text{in}_2}\right|_{\text{in}_1=0}\\ \left.S_{21}=\frac{\text{out}_2}{\text{in}_1}\right|_{\text{in}_2=0}\qquad\left.S_{22}=\frac{\text{out}_2}{\text{in}_2}\right|_{\text{in}_1=0} \end{aligned}\tag{1}$

$S_{11}$ 为输入端口电压反射系数， $S_{12}$ 为反向电压增益， $S_{21}$ 为正向电压增益， $S_{22}$ 为输出端口电压反射系数。（有的书上写的是功率波反射系数，这里考虑到回损 $\text{RL}$ 与 $-S_{11}$ 保持一致，故认为是功率比。如果认为是电压比，则用dB表示时乘以-10而不是-20）

$S$ 参数矩阵可用于确定双端口网络两侧的反射系数和传输增益。此概念可进一步拓展至确定多端口网络的 $S$ 参数。

根据 $S$ 参数矩阵各矩阵元，可以进一步确定增益、回波损耗、电压驻波比(VSWR)和插入损耗。

回波损耗RL

又称为反射损耗（工程上与 $-S_{11}$ (功率比)数值保持一致），越小越好，这样反射回来的功率波就越小。电缆链路由于阻抗不匹配会产生功率波反射，功率波反射会与输入的功率波叠加产生驻波。若反射的功率波振幅与输入的相同，则会形成完全的驻波。

输入电压 $U_0\cos(kx-\omega t)$ ，反射系数 $\Gamma$ （功率下 $S_{11}=20\log\Gamma$ ），则反射电压为 $\Gamma U_0\cos(kx+\omega t)$

$\left\{ \begin{aligned} U_0\cos(kx-\omega t)+\Gamma U_0\cos(kx+\omega t)&=(1-\Gamma)U_0\cos(kx-\omega t)+2\Gamma U_0\cos\omega t\cos kx\\ &=(1+\Gamma)U_0\cos\omega t\cos kx+(1-\Gamma)U_0\sin\omega t\sin kx\\ &=U_0\sqrt{1+\Gamma^2+2\Gamma \cos2\omega t}\cdot\sin(kx+\theta)\\ \tan\theta&=\frac{1-\Gamma}{1+\Gamma}\tan\omega t \end{aligned} \right.\tag{2}$

由（1）式可知，当反射系数 $\Gamma$ 为1时形成完全的驻波，此时功率波无法通过链路，能量始终存储于驻波内部。当 $\Gamma$ 小于1时，部分功率波以电磁辐射的形式发射出去，反射回去的功率波与前向传输的功率波形成了行驻波，驻波存在最大和最小幅值，回波损耗为 $\Gamma^2$ ，换算成dB单位就是 $-20\log\Gamma$ dB。

电压驻波比VSWR

又称为驻波比，介于1到 $\infty$ 之间，代表反射功率波与前进功率波形成的行驻波的最大和最小幅值之比。根据回波损耗的计算公式，行驻波的幅值为

$U=U_0\sqrt{1+\Gamma^2+2\Gamma\cos\omega t}\tag{3}$

该幅值存在最大值 $(1+\Gamma) U_0$ 和最小值 $(1-\Gamma)U_0$ ，驻波比就是该幅值的最大和最小值比 $U_\text{max}/U_\text{min}=(1+\Gamma)/(1-\Gamma)$ ，拓展到复数域 $(1+|\Gamma|)/(1-|\Gamma|)$ 。根据该式可知，当反射系数 $\Gamma$ 趋近于1时，驻波比趋近于无穷大，此时功率波无法通过负载链路；当反射系数趋近于0时，VSWR趋近于1，此时几乎所有功率波以电磁辐射的形式发射出去。

驻波比与回波损耗的关系

$\left\{ \begin{aligned} \text{RL}&=\Gamma^2\\ \text{RL(dB)}&=-20\log\Gamma=-20\times\log\frac{\text{VSWR}-1}{\text{VSWR}+1}\\ \text{VSWR}&=\frac{1+|\Gamma|}{1-|\Gamma|}=\frac{10^{\frac{\text{RL}}{20}}+1}{10^{\frac{\text{RL}}{20}}-1}\\ \end{aligned} \right.\tag{4}$

插入损耗IL

在传输系统某处由于元件或器件的插入而发生的负载功率的损耗，它表示为该元件插入前负载上接收功率与插入后同一负载接收功率以分贝为单位的比值。

$\text{IL}=-10\log(P_o/P_i)=-20\log|S_{21}|\ \text{(dB)}\tag{5}$

插入损耗是指发射机与接收机之间插入电缆或元件产生的信号损耗；
插入损耗指功率方面的损失，衰减指信号电压幅度相对测量插入损耗电路原信号幅度的降低。
若 $S_{21}$ 为功率比，则 $S_{21}$ 转为dB时需要乘以-10而不是-20。

阻抗匹配

微波电子学的一部分，主要用于传输线上，来达至所有高频的微波信号皆能传至负载点的目的，几乎不会有信号反射回来源点，从而起到保证设备正常工作、提升能源效益、避免信号失真、增强信噪比的作用。

阻抗匹配有两种，一种是通过改变阻抗（用于集总参数电路），另一种则是调整传输线的波长（用于传输线）。
- 集总参数电路又称集总电路，由许多由电源、电阻、电容、电感等集总元件所组成的电路;
- 集总元件是指元件大小远小于电路工作频率相对的电磁波波长时的所有元件，类似慢变振幅近似，可认为元件工作在静态场，此时对信号而言，不论何时元件特性始终保持固定，与频率无关。若元件大小与电路工作频率相对的电磁波波长差不多或更大时，则元件特性因信号频率不同而变化，即慢变振幅近似失效，可认为元件工作在动态场，元件内部电子或晶格对场的作用响应不过来，此时不能将元件整体视为特性固定的单一体，而应称为分布元件。这里的集总和分布针对的是工作频率，集总是集所有频率的总体特性，分布是在不同频率的特性分布。在微波电路中，传统导线很可能成为具有电感及电容串并联特性的复杂组合。
要匹配一组线路的阻抗，首先把负载点的阻抗值，除以传输线的特性阻抗值来做归一化，然后把数值划在史密斯图上。
- 史密斯图是一种用于电子工程的图表，工程师用它解决传输线和阻抗匹配电路的相关问题，可以将射频电路的多种参数显示在内。显示的电路参数包括阻抗、导纳、反射系数、散射参数（S参数）、等噪声圆、等增益圆、稳定圆等。
- 史密斯图是对二维直角坐标系的复平面数学变换。阻抗实部为正的数映射在单位圆内，负的映射在外，通常人们关注的是圆内，不考虑电阻为负的情况。该数学变换映射的量为 $S_{11}$ ，代表线路的反射系数，即S参数里的 $S_{11}$ （电压比）
  
  $\left\{ \begin{aligned} S_{11}&=\frac{Z_L-Z_0}{Z_L+Z_0}=\frac{z-1}{z+1}\\ z&=\frac{Z_L}{Z_0} \end{aligned} \right.\tag{1}$
  
  式中 $Z_L$ 为电路的负载阻抗值， $Z_0$ 为参考阻抗值（系统阻抗），一般选择传输线的特性阻抗，通常为50 $\Omega$ ， $z$ 为归一化阻抗。史密斯图中图表原点为1，即满足阻抗匹配。使用归一化阻抗描述史密斯图的优点是让同一张史密斯图适用于特性阻抗不同的各种系统。
- 史密斯图原理如下
  
  电磁波顺着特性阻抗 $Z_0$ 的传输线前进，在末端遇到一个阻抗 $Z_L$ 的负载（归一化阻抗 $z=Z_L/Z_0$ ）。此时信号会发生反射，反射系数为 $\Gamma$ 。史密斯图上的任意一点同时表示阻抗值 $z$ （左图）和对应反射系数 $\Gamma$ （右图）。ADS中的史密斯图， $\Gamma$ (这里指代电压比 $S_{11}$ )是以xx/xxx的形式表现的，其中xx代表幅值，xxx代表相位，整体以复指数的形式展现。