哈密顿量和正则方程
哈密顿量和正则方程
-
哈密顿量是什么,为什么要有哈密顿量?
哈密顿量是拉格朗日量的勒让德变换:
拉格朗日量是在广义坐标和广义速度空间对系统能量的表述,适用拉格朗日量表述的力学系统称为拉格朗日系统,可用拉格朗日方程组对系统状态进行求解。
哈密顿量是在广义坐标和广义动量空间对系统能量的表述,使用哈密顿量表述的力学系统称为哈密顿系统,可用哈密顿正则方程对系统状态进行求解。哈密顿量存在的意义是用广义动量(也称为共轭动量)作为变量取代广义速度(),这样就能处理特定的复杂系统,例如使用概率波函数描述粒子状态的量子系统。
-
什么是勒让德变换,为什么哈密顿量是拉格朗日量的勒让德变换?
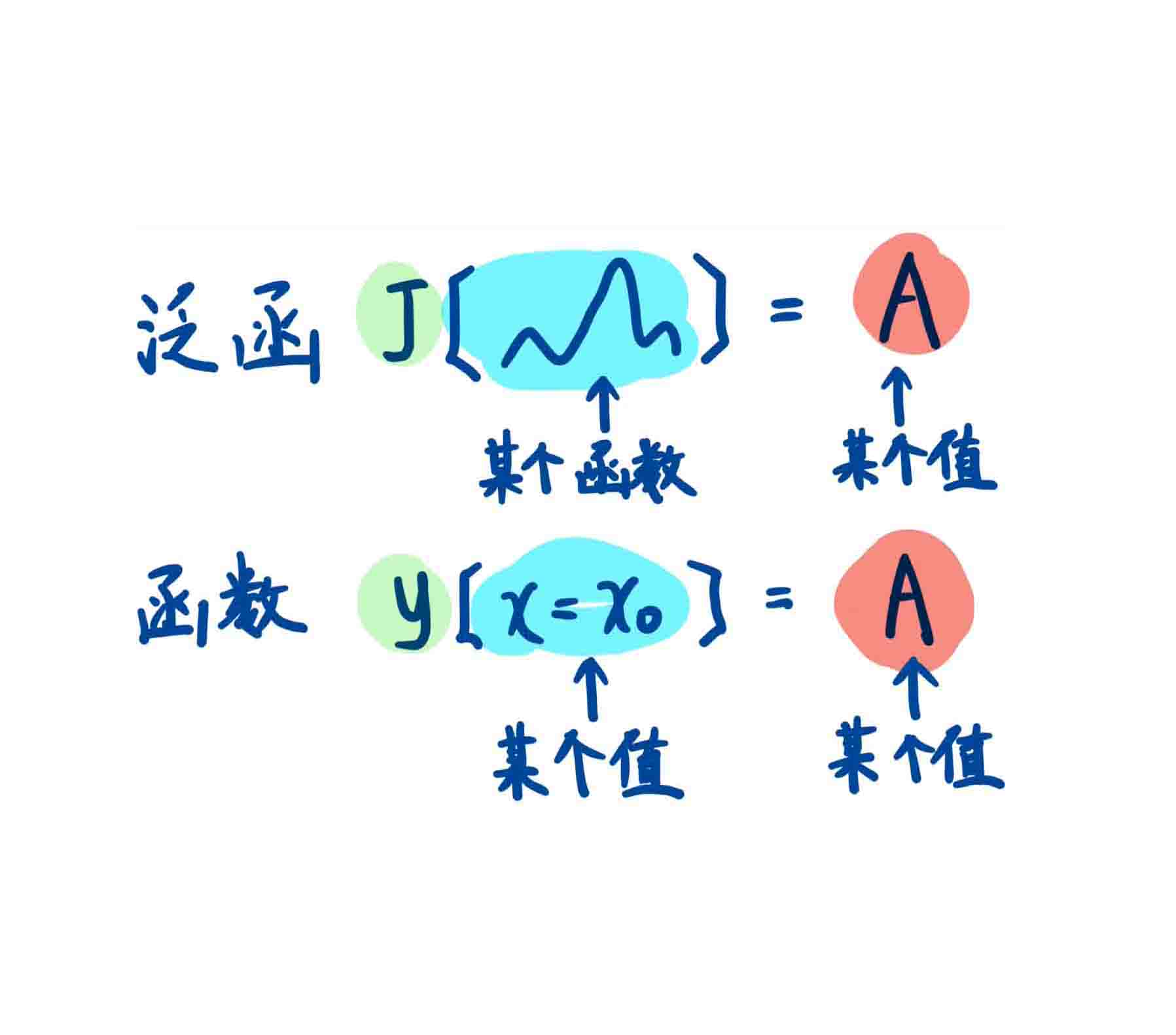
勒让德变换是一种在不改变系统状态和细节的前提下,替换变量元的数学换元法。以单变量函数为例,函数在处斜率为,那么对应存在经过该处的切线与轴()相交的截距,和存在一一映射关系。在这种映射之后,原本的变量由变换成了斜率,根据斜率和该点的位置信息可以获取截距信息。
拉格朗日量是对系统能量状态的表述,在对系统进行分析时,需要经常进行全微分操作:
令,则
对做全微分:
代入哈密顿方程组和广义动量的定义
得到哈密顿正则方程
-
为什么要用勒让德变换将拉格朗日量转变为哈密顿量?
假定存在映射关系,但该关系无法用显式表达,我们只知道x和y一一对应的值,这在实际的运算和分析当中将非常不便。利用勒让德变换将x和y的关系转换为无数个切点切线的组合,将无法用显式表达的关系切割成无数个线性关系的叠加,既简化了映射关系的表述,又保留了映射关系的细节,体现了物理中变换不能改变事物发展细节的思想。根据前面的内容,可以看到哈密顿正则方程组是一阶微分方程,比拉格朗日方程组更容易求解(后者二阶)。通过勒让德变换,引进动量维度,使得系统的运动方程更加简洁清晰。
评论