HSD 基础(三&四)

High-Speed Links Circuits and Systems

第三章

测量互连模型的技术主要有两种

时域反射仪（TDR），时域
矢量网络分析仪（VNA），频域

TDR（Time-Domain Reflectometer）

TDR 由一个快速阶跃电压信号发生器和一个高速示波器构成
TDR 操作
- 输出快速阶跃电压信号至待测通道
- 观察源的电压反射信号
- 通过电压幅值计算出阻抗
- 阻抗不连续的位置依靠时延来确定
仅能从输入端口连接需要表征的通道

TDR 阻抗计算

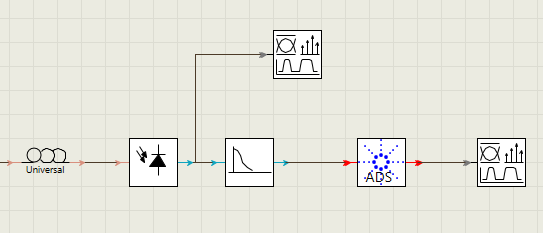
ADS仿真TDR

TDR的上升时间和分辨率

TDR 的空间分辨率由阶跃上升时间所设定

$\Delta x>t_rv$
阶跃上升随传输通道衰减
- 趋肤效应引起的色散
- 集总元件不连续会对阶跃信号产生低通滤波的作用
对于估计 L & C 的参数造成困难
通道滤波器可以对集总元件不连续产生的尖峰进行补偿

TDR多重反射

TDT（Time-Domain Transmission）

TDT 可用于测量传递函数

$H(j\omega)=\frac{V_2(j\omega)}{V_1(j\omega)}$

很难隔离开阻抗不连续的点位，因为它们是同时叠加在同一个上升沿上的

网络分析仪（Network Analyzer）

扫频激发源产生信号输入通道网络
测量网络的相应幅度和相位
能够测量传递函数，散射矩阵参数，阻抗，…
测试信号集根据不同的测量用途进行配置

定向耦合器

高频网络分析仪中的测试信号集需要使用定向耦合器
定向耦合器由两条在短距离内相互耦合的传输线构成
恰当设置耦合长度能够使 $Z_A$ 两端电压与前向行波成正比， $Z_B$ 两端电压与反射波成正比

传递函数与阻抗测量

Transfer Function and Impedance Measurements

传递函数测量
- 输入信号来自一个定向耦合器，该耦合器对前向行进波进行采样
- 待测网络的输出即为输出结果
阻抗测量
- 输入信号来自一个定向耦合器，该耦合器对前向行进波进行采样
- 将来自网络的反射波与该输入进行比较，以表征频率范围内的阻抗

散射参数（S Parameter）

基本定义略过

主要注意级联 S 参数

网络分析允许将独立表征的结构进行级联
然而，不能直接级联 S 参数矩阵并相乘
必须首先将S参数矩阵转换为 ABCD 矩阵（或 T 矩阵）

ABCD 参数

ABCD 参数可以看作无端接下的 S 参数，但并非无端接，而是单纯考虑输入和输出电压电流的关系。正规 S 参数的计算必须要有双端端接，否则电压源会将输入稳压，反射信号无法吸收，接收端则负载短路。

级联 S 参数时，将考虑端接的 S 参数转化为无端接的 ABCD 参数，再进行矩阵相乘，从而消除端接的影响。

冲激响应

通道冲激响应用于
- 时域仿真
- 链路分析工具
冲激响应与 S 参数互为傅里叶变换关系

$h(t)=\mathcal{F}^{-1}\{S(\omega)\}$
为了提高冲激响应的分辨率，可以将 S 参数的频域范围拉大并用 0 来填充（Zero Padding）

通道瞬态响应

通道波形输出为输入波形与通道冲激响应的卷积

眼图

第四章

ISI 和通道脉冲模型

ISI（Inter-Symbol Interference）

前一个比特的残留状态会使当前比特产生失真，由此造成码间干扰
ISI 是由反射，通道谐振，通道损耗（色散）导致
冲激响应与输入波形的卷积即为输出波形

$y^{(1)}(t)=c^{(1)}(t)*h(t)$

NRZ 数据建模

一个 NRZ 数据流可以建模为独立的“0”和“1”的叠加
通道响应到 NRZ 数据流等价于各个独立冲激响应的叠加

通道冲激响应

得到了通道的冲激响应，便可以计算码元的原始波形对应的通道输出波形。最后再将码元波形按照码元时序进行叠加，便得到了整个传输数据的输出波形。

通道的有限冲激响应（FIR）模型

峰值失真分析

分析脉冲响应，能够估计最差情况下的眼高和数据码型
最差情况下的“1”，由一个“1”脉冲幅值和所有 $k\neq0$ 的负脉冲响应之和叠加而成

$s_1(t)=y_0^{(1)}(t)+\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(d_k)}(t-kT)\bigg|_{y(t-kT)<0}$

最差情况下的“0”，则由一个“0”脉冲幅值和所有 $k\neq0$ 的正脉冲响应之和叠加而成

$s_0(t)=y_0^{(0)}(t)+\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(d_k)}(t-kT)\bigg|_{y(t-kT)>0}$
最差情况下的眼高为

$\begin{aligned} s(t)&=s_1(t)-s_0(t)\\ &=(y_0^{(1)}(t)-y_0^{(0)}(t))+\left(\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(d_k)}(t-kT)\bigg|_{y(t-kT)<0}-\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(d_k)}(t-kT)\bigg|_{y(t-kT)>0}\right)\\ &=2\left(y_0^{(1)}(t)+\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(1)}(t-kT)\bigg|_{y(t-kT)<0}-\sum_{\substack{k=-\infty\\k\neq0}}^{\infty}y^{(1)}(t-kT)\bigg|_{y(t-kT)>0}\right) \end{aligned}$

这里由于“1”和“0”的脉冲对称，有

$y_0^{(0)}(t)=-1(y_0^{(1)}(t))$

眼高为正，则眼图睁开，否则眼图闭合。

比较 NRZ（PAM-2）和 PAM-4 调制

NRZ
- 最简单常见的调制格式
PAM-4
- 一个符号传输两个比特信息
- 传输同样比特信息仅需 NRZ 一半的速率，通道均衡和线路需求更少
- 编码格式类似格雷码，即相邻振幅的编码仅有一位不同
- 信号带宽仅为 NRZ 的一半

奈奎斯特频率

奈奎斯特带宽限制
- 理论上探测无码间干扰且符号率为 $R_s$ 的信号，需要系统带宽为 $R_s/2$ ，采样率为 $R_s$
- 奈奎斯特频率的定义为：离散信号系统采样过程中，能够完整重建原始连续信号所允许的最高频率。由于对连续信号进行离散采样处理会使信号频谱产生周期延拓，为使频谱不产生混叠，采样信号频率需要为奈奎斯特频率的两倍。也可以认为，奈奎斯特频率的计算式为采样信号频率的一半
- 频率混叠的结果和码间干扰 ISI 的区别和联系：
  1. 频率混叠在时域的表现是高频信号“折叠”到低频区域，使采样得到的离散信号失真，这种偏差不一定直接对应 ISI
  2. 频率混叠是模拟信号采样过程中的问题，影响波形，ISI 是数字信号的问题，影响误码率
  3. 频率混叠造成波形失真会进一步影响码间干扰

考虑使用 PAM4 编码的情况：

通道插损超越了 PAM-4 编码造成的眼高折损代价

插损大于 $20\times \log_{10}\frac{1}{3}=-9.54 \ \mathrm{dB}$ 时用PAM-4编码

片上时钟速率限制

PAM2 优于 PAM4	PAM4 优于 PAM2

带宽 2.5 G 的通道可允许 5 G 的 PAM-4 信号无 ISI 传输；带宽 5 G 的通道可允许 10 G 的 PAM-2 信号无 ISI 传输
根据通道响应可确定不同带宽位置处的损耗，若 PAM-2 与 PAM-4 带宽处损耗差值小于 -9.54 dB，则 PAM-2 受带宽影响代价小于 PAM-4 编码造成的代价，此时用 PAM-2，即 NRZ 编码。反之插值大于 -9.54 dB，则用 PAM-4 编码。